ビジネス統計スペシャリスト対策！Excelで基本統計量を求める操作方法

2021年11月6日

はじめに

今回はビジネス統計スペシャリストにも役立つ、Excelで基本統計量を求める操作方法とデータの見方について解説します。

基本統計量というのはデータ群の平均や標準偏差のように一つの指標を表すものではありません。

詳しくは後ほど解説しますが、つまるところ基本統計量はデータのプロフィールと考えてもらえれば間違いないでしょう。

それでは早速、操作方法について解説をしていきます！

「ビジネス統計スペシャリストってなに？」という方は下記の記事を参考にして下さい。

【ビジネス統計スペシャリストに合格】統計検定との違い、難易度、メリット　解説しま

こんなひとに読んでほしい 統計検定との違いを知りたいひとビジネス統計スペシャリストのメリットを知 ...

 https://machuken.com/post-497/

操作方法

基本統計量を算出するにあたり、下記の例題を使用します。

今回のように東京・大阪といったデータ群の数値的特徴を捉えるには基本統計量がぴったりです。

「東京の店舗数は？」
「大阪の店舗の売り上げ平均は？」
「店舗ごとの売り上げのバラつきは大きいかな？」
「県内でちょうど真ん中の売り上げは？」

このほかにもたくさんのことを同時に計算してくれます。まずは東京と大阪を比較するためには様々な指標を揃えて、何を比較して企画につなげていくかが大切です。そのために使うのが基本統計量というツールです。

「君ってどんなデータなの？」という疑問を解決してくれます。

まさに基本統計量はデータのプロフィールであるということが分かりますね。

Excelで基本統計量を求めるにはデータ分析ツールを使うのですが、初期設定のままでは使用することができません。簡単な操作で機能解放できますので、まだの方は参考にして下さい。

【ビジネス統計スペシャリストに合格】Excelにデータ分析ツールを導入する方法

はじめに この記事では下記の２点が分かります。 この記事で分かること １：Excelでデータ分析ツールを ...

 https://machuken.com/post-722/

基本統計量ツールを選択

Excelを立ち上げたらデータ分析ツールの基本統計量を選択します。

範囲指定をする

分析するデータの範囲を指定します。指定する選択列は東京～大阪、選択列は数字の入っている最終行までを選択して下さい。上の図の太い四角で囲まれた部分は全て選択範囲です。範囲指定をしたあとは必ず先頭行をラベルとして使用と統計情報にチェックを入れて下さい。

先頭行をラベルとして使用 とは

指定した範囲の先頭列に数字以外のデータを入れた場合は必ず先頭行をラベルとして使用にチェックを入れましょう。これはExcelに対して「先頭行のデータは分析対象のグループ名だよ」と伝えることになります。チェックを入れ忘れると上の画像のようなアラートが出ます。

結果がでました！

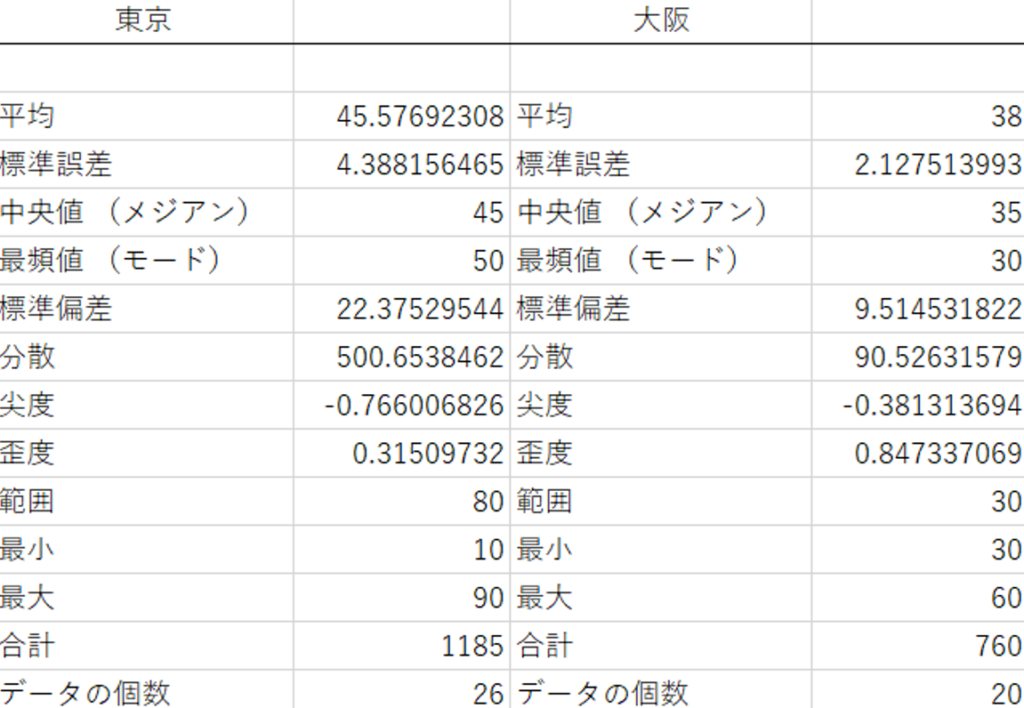
お疲れさまです！結果が出ました。

データから分かること

それでは先ほど算出したデータについて、それぞれの意味がわかるように解説をしていきます。

平均、合計、データの個数

各データ群の平均、合計、そしてデータ数を表しています。東京のデータで例えるならば、「東京の全26店舗の平均売上は45.6万円、合計で1185万円」といえます。

最小、最大、範囲

最小、最大は各データ群、つまり東京・大阪それぞれの地方で一番売上の高い店舗と低い店舗の金額です。範囲は最大と最小の幅を表します。これらの値を平均と組み合わせることで「東京は売上にバラつきがある一方、大阪はそんなに開きがないな。平均の売り上げを見ても明らかだ」みたいなことが推測できたりします。

中央値、最頻値

中央値は、各データ群の個体を売上順にならべたときに、左から数えてちょうど真ん中に位置する店舗の売り上げです。今回の例では東京は全部で26店舗ですね。これを売上の少ない準備に一旦並び替えます。店舗数のちょうど真ん中、13店舗目と14店舗目を足して２で割った値が中央値です。これが奇数、25店舗であれば13店舗目がちょうど真ん中にきます。

最頻値は、各データ群に一番多く登場する数値です。東京は50万円の売り上げの店舗が一番多いことになります。

標準偏差、標準誤差

統計学を学んでいないと聞きなれないワードですね。標準偏差とは、各データ群の平均に対してのバラつきを表しています。東京を例に簡単に言うと、「東京のどの店舗も、45.6万円に対して前後22.4万円の売り上げである」ということです。加えて大阪の標準偏差は9.5万円ですので、「大阪は東京に比べて店舗ごとの売り上げのバラつきが少ないな」ということが分かります。

一方、標準誤差とはなんでしょうか。標準誤差は一言で表すと、「標準偏差から標準誤差の数値分だけ前後しますよ」と言っています。

意味が分かりませんね。

実のところ今回の例で標準誤差はあまり使いどころがありません。というのも、今回は全店舗の売り上げが分かり切っていますので標準偏差が前後しないのです。もしこれが東京の50店舗から抜き出した26店舗、みたいなことであれば標準偏差は26店舗分と50店舗分で前後する可能性があるので標準誤差は有効な考え方になります。

ちょっとクドい言い方をしますと、「26店舗の中では（26店舗の）平均売上に対して前後22.4万円のバラつき（標準偏差）があった。もし50店舗のバラつき（標準偏差）を出したら（50店舗の）平均売上に対して22.4万円の前後4.4万円（標準誤差）の間の数値がでる」ということになります。

尖度、歪度

最後に尖度（せんど）と歪度（わいど）ですが、こちらの説明には統計学の用語を交えての解説がどうしても必要になりますので、「こんな感じなんだな」とだけ思っていただければ大丈夫です。

皆さんは上のようなグラフをご覧になったことはあるでしょうか。ヒストラグラムと呼ばれるものです。その中でも左右対称できれいな山の形をしたヒストグラムを正規分布といいます。

例えばクラスのテストの点数を思いだしていただけるとわかりやすいのですが、100点満点のテストを実施した場合、少数の成績上位者と下位者、そして多数の中間層がいたと思います。確率理論というのはこの正規分布を中心に考えることが多く、少数の特異な現象と大多数のよくある現象という前提から、自身が抽出したデータがどれだけ正規分布に近いのか・遠いのか、みたいなことを考えたりします。尖度・歪度もその一環だと思って下さい。

上のヒストグラムは東京の26店舗の各売上を売上ゾーンに区切ったときに、そのゾーンに何店舗が該当するのかを見える化したものです。尖度・歪度というのは、このグラフが正規分布に対してどれだけ尖っているか（尖度）、左右に歪んでいるか（歪度）を数値で表したものになります。

尖度・歪度ともに値は0を起点として、尖るほどプラス、凹むほどマイナス、左に歪むほどプラス、右に歪むほどマイナスに近づきます。

今回の結果では東京の尖度が-0.77、歪度は0.31でした。つまり正規分布ほど山は尖っておらず、左に歪んでいることがグラフを見なくてもわかります。

「全体的に平坦で、売上の少ない店舗がやや多いな」みたいなことが言えたりします。

まとめ

今回は基本統計量の求め方と、各種指標から分かることについて解説をしました。統計学といってもその用途は幅広く、今回のように一般的な業務の中でも活用できることはお分かりいただけましたでしょうか。各項目とも数式や用語を抑えて説明していますので、正直これらの説明では学問としての理解には及ばないかもしれません。

「座学でガッツリやりたい！」という方にはうってつけの資格があります。統計検定です。

その中でも今回ご紹介した基本統計量を学ぶのに最適なのは２級と３級です。それぞれの資格対策については別記事で細かく解説していますので気になる方はお読み下さい。

【出題範囲が増えて難しくなった！】統計検定３級から受けるべき３つの理由

こんなひとに読んでほしい 統計検定２級と３級のどちらを受験するか迷っているひと学生時代に数学が苦 ...

 https://machuken.com/post-241/

【統計検定２級に合格】勉強期間別の学習パターン３選　対策方法をご紹介します

こんなひとに読んでほしい 統計検定の受験がはじめてのひと統計検定２級を最短・最小コストで突破した ...

 https://machuken.com/post-253/