ビジネス統計スペシャリスト対策!ExcelでF検定を求める操作方法

●ExcelでF検定を行う方法
●データの読み取り方
はじめに
ご訪問ありがとうございます!まちゅけんです
ヨメちゃんです
今回はビジネス統計スペシャリストにも役立つ、ExcelでF検定を行うための操作方法とデータの見方について解説します。
F検定を一言でいうと、「AチームとBチーム、各チーム内の数値のバラつきは、AチームとBチームで同じか?」ということを調べる行為です。
統計学の用語を使って言い換えると、「2つのデータ群の分散は等しいか・そうではないか」とも説明できます。分散分析とか言ったりします。
実はこのF検定ですが、単独で使うことはテストでもない限りはあまり機会がありません。多くの場合、t検定という別の分析とセットで使用します。
t検定に関する説明はまた別の機会にお話をさせていただくとし・・・
早速、F検定の操作方法について解説をします。
「ビジネス統計スペシャリストってなに?」という方は下記の記事を参考にして下さい。
操作方法
F検定を行うにあたり、下記の例題を使用します。
あなたは食品メーカーの商品開発担当です。この度、あなたが担当するカップラーメン部門で新商品を開発することになりました。開発部長からは、地域の特性にあった商品を提案してほしいと依頼されています。まずは参考として既存商品の人気調査から始めました。既存の商品は一つのカップラーメンでも薄味・濃い味で2種類の商品を東京と大阪で展開しています。
部長「今回は東京と大阪で、同じ商品だけど味付けが違うものを限定で展開したいと思うんだ。既存商品を参考に、人気の味付けで評判の良い方をそれぞれの地域に展開したいと思うんだけどどうかな?」
あなた「データさえあれば可能ですね」
部長「ということであれば、既存商品の味付け別に東京・大阪それぞれ10人にアンケートを取ったデータがあるよ。評価は1~5点。使えそうかな?」
あなた「任せて下さい!これがあれば東京・大阪にそれぞれに最適な商品が分かるかもしれません」
| 薄味 | 濃い味 | |
|---|---|---|
| 東京 | 4 | 4 |
| 東京 | 4 | 5 |
| 東京 | 5 | 1 |
| 東京 | 4 | 4 |
| 東京 | 5 | 5 |
| 東京 | 4 | 1 |
| 東京 | 5 | 5 |
| 東京 | 4 | 1 |
| 東京 | 3 | 4 |
| 東京 | 4 | 5 |
| 大阪 | 5 | 5 |
| 大阪 | 4 | 4 |
| 大阪 | 4 | 4 |
| 大阪 | 5 | 5 |
| 大阪 | 4 | 4 |
| 大阪 | 5 | 4 |
| 大阪 | 4 | 5 |
| 大阪 | 5 | 5 |
| 大阪 | 4 | 5 |
| 大阪 | 4 | 4 |
ExcelでF検定を行うにはデータ分析ツールを使うのですが、初期設定のままでは使用することができません。簡単な操作で機能解放できますので、まだの方は参考にして下さい。
F検定:2標本を使った分散の検定を選択
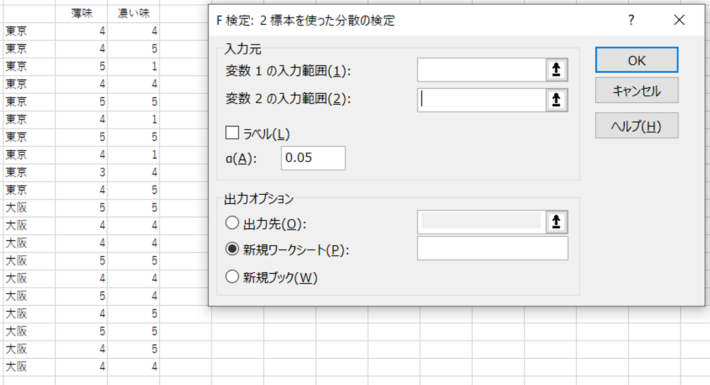
Excelの分析ツールを開き、「F検定:2標本を使った分散の検定」を選択します。
範囲指定をする
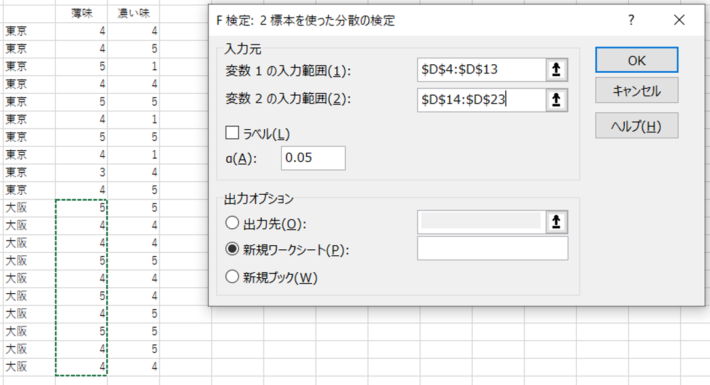
今回の検定では2通りの検定を行います。
1回目の検定では・・・
変数1の入力範囲に薄味×東京10名
変数2の入力範囲に薄味×大阪10名
※薄味に対する東京・大阪の評価のバラつきを比較
2回目の検定では・・・
変数1の入力範囲に濃い味×東京10名
変数2の入力範囲に濃い味×大阪10名
※濃い味に対する東京・大阪の評価のバラつきを比較
をそれぞれ調べます。
結果が出ました!
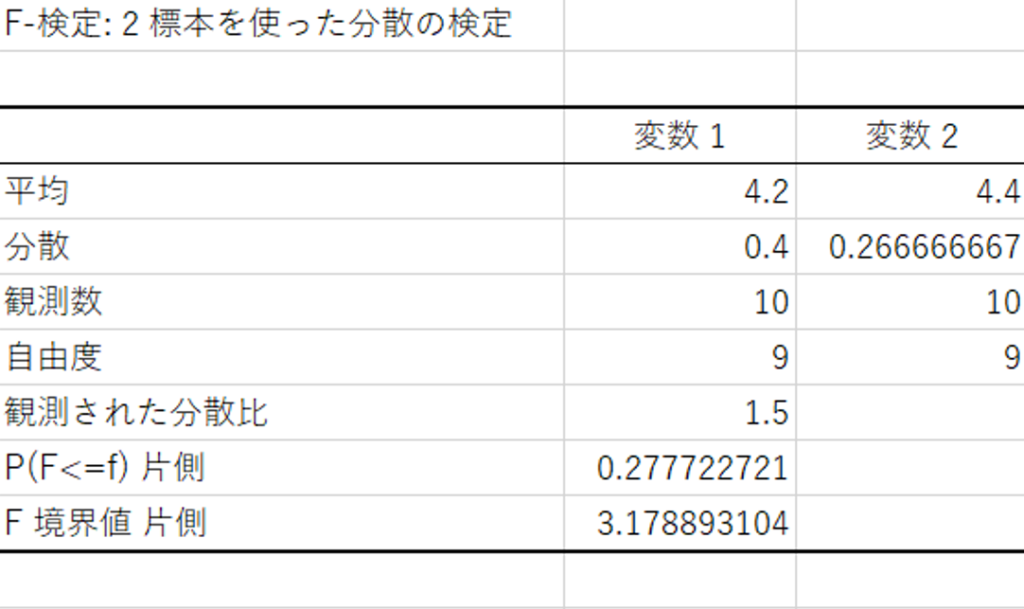
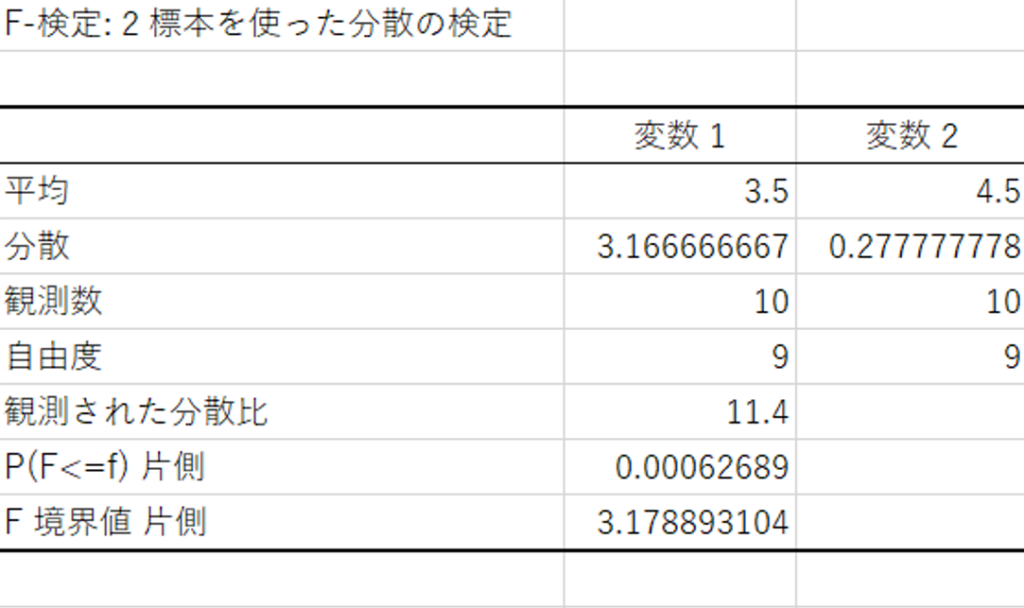
おめでとうございます!結果がでました!
これだけ見てもよくわからないな
見るところは限られているから大丈夫だよ
データから分かること
今回の結果で見るべき箇所はたったの一つ
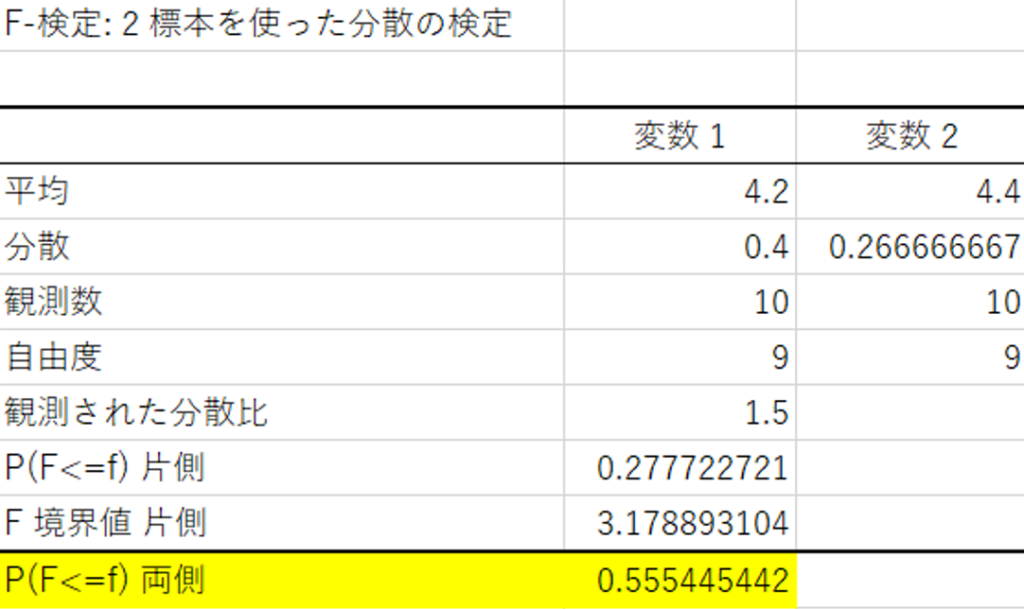
P(F<=f)片側だけです。
この値をP値といいますが、P値はパーセンテージに置き換えることができます。
P値を2倍にして0.05(5%)よりも大きけれ変数1と変数2のバラつきに違いはあったとしても「誤差程度」ですし、逆に小さければ変数1と変数2のバラつきは「明確に異なる」と判別をします。
ちなみに「5%」という数字がどこから出てきたのかというと、統計学ではこの値を有意水準といいます。有意水準は自由に設定することができますが概ね5%で設定をします。「検定結果が5%を切ったら、東京と大阪の評価のバラつきに違いがあるのは有意(意味が有ること)にしよう。それ以上の数字が出たら偶然として処理しよう」と考えます。
P(F<=f)片側を2倍する
「なぜ2倍?」
と思ったかもしれません。こちらの説明をするには帰無仮説・対立仮説・片側検定・両側検定の概念を説明する必要があります。
しかしビジネス統計スペシャリストではそこまで深く突っ込んだ部分は問われないことを考えるとこちらでの説明は省略します。
統計検定2級の受験者向けに「簡単な片側検定と両側検定の見分け方」について解説した記事があるので気になる方はご参考程度にお読みください。
帰無仮説が「2つのデータ群の分散に違いはない」、対立仮説が「2つのデータ群の分散に違いがある」と思いながら読むとお分かりいただけるかもしれません。
先ほどからパーセンテージと言っていますが、これが一体なんの確率かわかりませんよね。
1つめの検定を例にあげていえば
「薄味に対する東京と大阪の評価のバラつきに違いがあるのは0.56(0.28の2倍)の確率でたまたま」
ということができます。
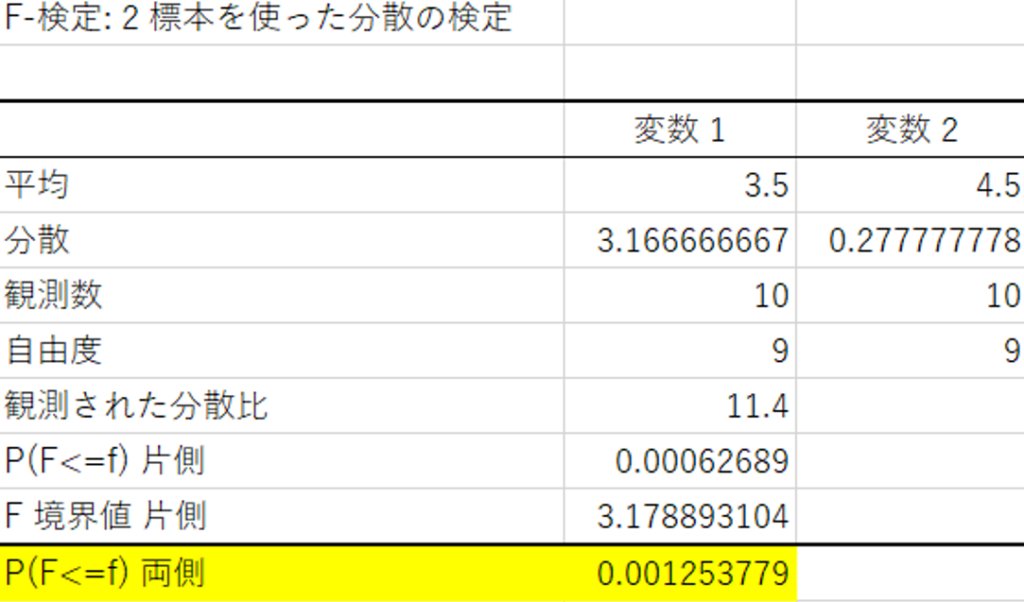
なので2つ目の結果からは、
濃い味に対する東京と大阪の評価のバラつきには違いがあるので、「東京と大阪のどちらかでは濃い味は賛否両論なんだろうな」みたいなことが分かったりします。
たしかによくデータを見ると、薄味は東京・大阪ともに評価が高い一方で、濃い味は東京で賛否が分かれています。
なので「よし東京では思い切って薄味だけ、大阪では濃い味だけ売ろう」といった判断の材料にすることができます。
注意点
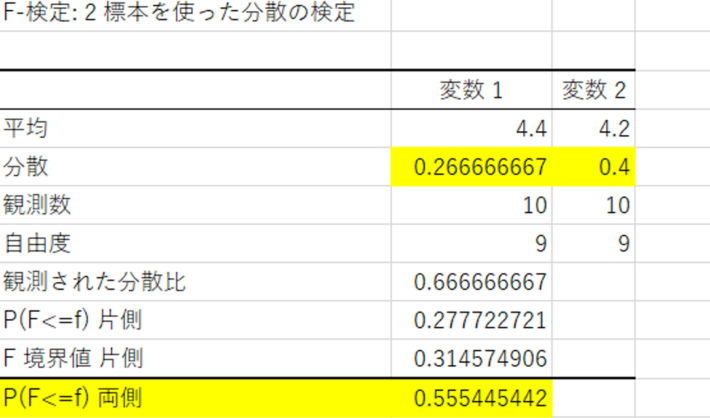
Excelの分析ツールでF検定をする際の注意点です。黄色く塗った分散という箇所をご覧ください。分析をする際は分散の値が、変数1>変数2となるように計算をして下さい。上記画像のように逆転させるだけでF境界値が全く関係のない数字になりますのでご注意下さい。
まとめ
今回はビジネス統計スペシャリストでも活用できる、Excelを使ったF検定の操作方法について解説をしました。実際の問題ではこのあとにt検定をして結果を求めさせるようなコンビネーション問題が出ることがほとんどだと思います。t検定については次回以降の記事で解説しますのでお待ちいただければと思います。
F 検定を解説するには統計学の用語や概念をかなりふんだんに盛り込む必要があるので、もしかしたら少しわかりづらい点があったかもしれません。
「座学でガッツリやりたい!」
と思った方は統計検定の受験をオススメします。なぜオススメするのかについては下記の記事でたっぷりと解説していますのでお読み下さい。
お読みいただきありがとうございました!
ありがとうございました!















ディスカッション
コメント一覧
まだ、コメントがありません