ビジネス統計スペシャリスト対策!スプレッドシートでヒストグラムを作成する方法

●スプレッドシートでヒストグラムを作成する方法
●ヒストグラムの超基本的な理解
はじめに
ご訪問ありがとうございます!まちゅけんです
ヨメちゃんです
今回はビジネス統計スペシャリストにも役立つ、スプレッドシートでヒストグラムを作成する方法とヒストグラムの基本的な解説します。
「ヒストグラムってなんですか?」
と思った方に向けて説明をすると・・・

↑こんな感じのグラフをヒストグラムといいます。
数値だけが書き込まれた表から、上記のようなヒストグラムを作るまでの方法を写真付きで例題を交えながら説明します。
「ビジネス統計スペシャリストってなに?」という方は下記の記事を参考にして下さい。
操作方法
ヒストグラムを作成するにあたり下記の例題を使用します。
あなたはとある小学校の学年主任です。担当する学年のA組とB組では定期的に学力テストを実施します。クラスの平均点を底上げするために、効果的な学習方法はないか考えることにしました。「A組とB組で学習スタイルを変えてみるのはどうだろう?」という作戦を考えます。そこであなたはつい先日実施された学力テストを両クラスで比較することにしました。点数は下記の通りです。
| 番号 | A組 | B組 |
|---|---|---|
| 1 | 0 | 10 |
| 2 | 5 | 35 |
| 3 | 10 | 30 |
| 4 | 10 | 55 |
| 5 | 20 | 50 |
| 6 | 30 | 40 |
| 7 | 35 | 45 |
| 8 | 30 | 50 |
| 9 | 50 | 50 |
| 10 | 55 | 55 |
| 11 | 45 | 50 |
| 12 | 40 | 45 |
| 13 | 50 | 55 |
| 14 | 55 | 50 |
| 15 | 70 | 45 |
| 16 | 60 | 40 |
| 17 | 70 | 70 |
| 18 | 75 | 75 |
| 19 | 80 | 95 |
| 20 | 100 | 90 |
スプレッドシートでヒストグラムを作成するにはデータ分析ツールを使うのですが、初期設定のままでは使用することができません。簡単な操作で機能解放できますので、まだの方は参考にして下さい。
データ分析ツールでHistogramを選択
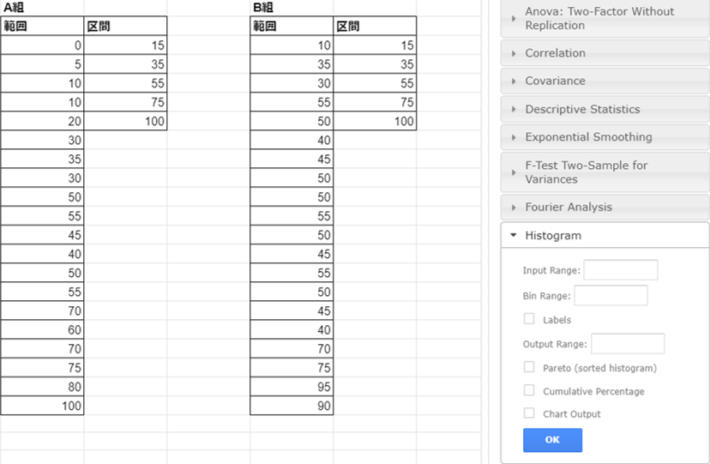
ヒストグラムとは「●点以上から●点未満」という区切りをつけて、その点数範囲に該当する個数をカウントしたものを棒状に積み上げたグラフのことを指します。そのため、上記図のようにあらかじめ点数の区間を設定しましょう。区間の設定は作成者の分析意図に沿って決めていただいて構いません。敢えて申し上げるとすればキリのいい数字にすることと区切り幅を統一してください。今回の場合はおおむね20点刻みでカウントしていきます。上記の図ではあえて分かりやすく点数・区間という名前をつけてもっともらしい表を作成しました。ですが皆さんが今後分析するにあたって上記のように区間を点数の横に書く必要はありません。極端な話、縦一列に点数、どこか離れたところに区切りたい数値を書くだけでも問題ありません。
入力範囲・データ区間を範囲指定する
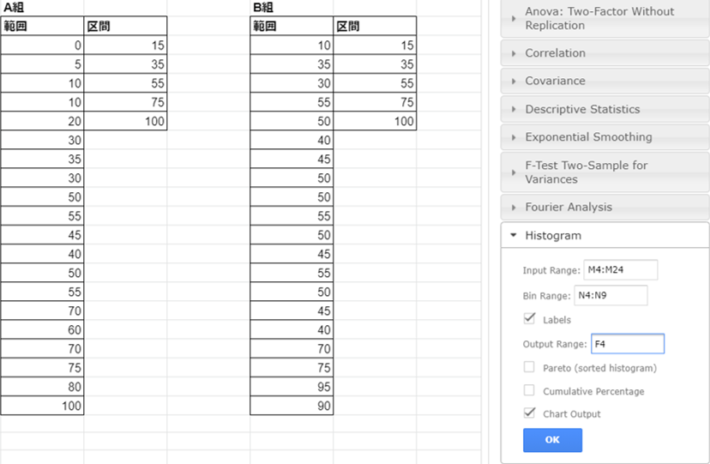
A組とB組のヒストグラムは別々に作成します。したがって同じ作業を二回行う必要があります。まずはA組からです。今回のケースでは数字の上に名前をつけました。入力範囲では「範囲~100」まで。データ区間は「区間~100」までを選択して下さい。選択範囲には数値以外も含まれているので必ずLabelsにチェックマークを入れて下さい。選択範囲が純粋な数値だけであればチェックを入れる必要はありません。
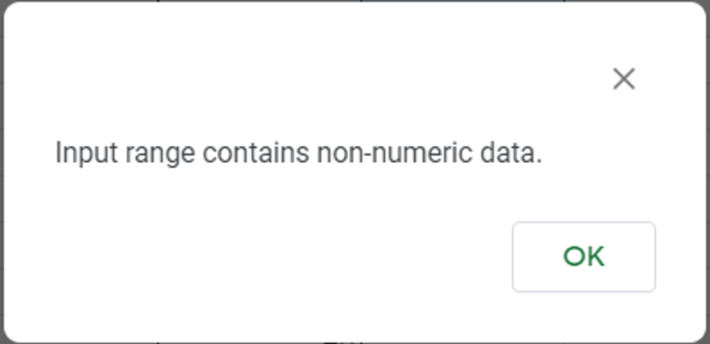
指定した範囲の先頭列に数字以外のデータを入れた場合は必ずラベルにチェックを入れましょう。これはスプレッドシートに対して「先頭行のデータは分析対象のグループ名・区間だよ」と伝えることになります。チェックを入れ忘れると上の画像のようなアラートが出ます。
ヒストグラムが完成しました!
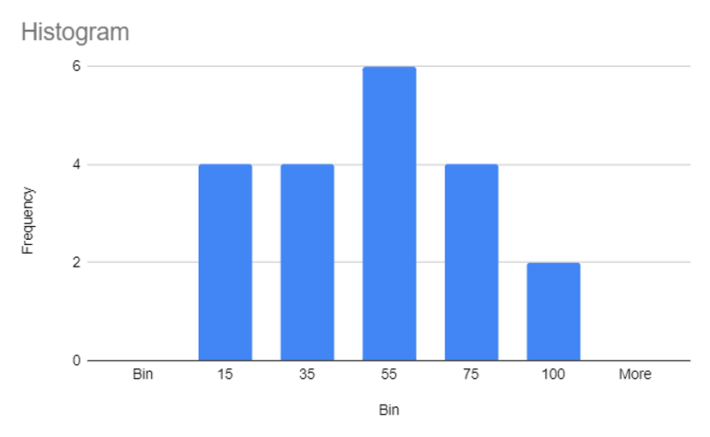
おめでとうございます!グラフを作成できました。
同じようにB組のヒストグラムも作成しましょう。
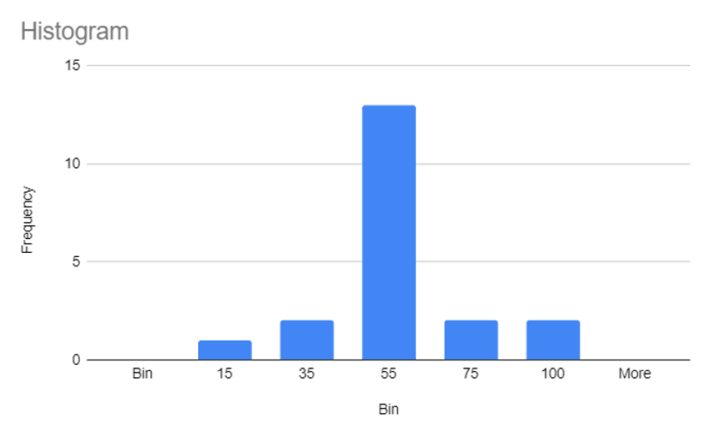
グラフを加工する
めでたくグラフを作成できましたが、実はもう一工夫が必要です。
上記で作成したした2つのグラフの縦の指標、頻度のメモリ幅を比較してみてください。度数は2刻みになっているものの、幅の広さが違うことがすぐにわかると思います。
※度数とは各区間に該当する数値の個数を表します。B組の結果を例にすると、0-15区間の度数は1、16-35区間の度数は2…といった具合に数えます。
2つのグラフを正しく比較するためにはこのメモリを等しくする必要があります。統計学ではこうしたグラフの見え方一つとっても意図せず誤解を与えたりすることがあるため、表現方法には注意しなければいけません。
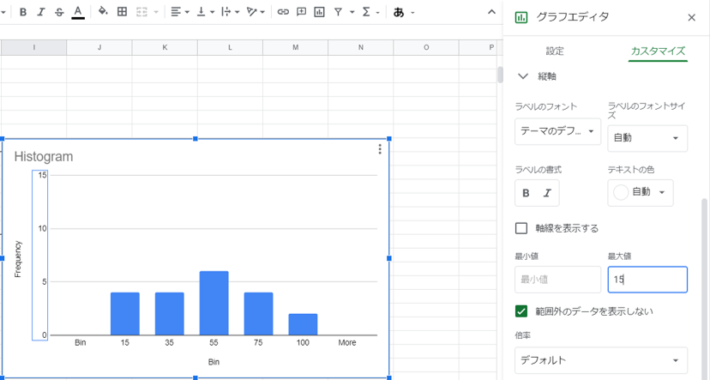
メモリ幅を変更するためには縦軸、Frequencyの横の数字を選択、ダブルクリックします。グラフエディタのカスタマイズが開きます。
少しだけ下にスクロールしたところにある最大値という項目で、縦軸の最大値を両グラフの大きい方に合わせます。今回のケースではB組の縦軸、15に合わせます。したがって最大値を15に変更します。
すると左右で並べたときに比較がしやすくなります。
ようやく完成です!
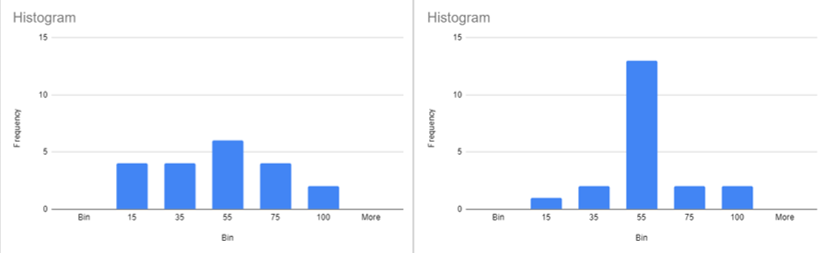
縦軸の最大値を揃えたことで左右に並べたときの比較がしやすくなりました!本当はこのあとに青い棒のグラフの間隔を詰めてくっつけるのですが、スプレッドシートでの間隔の詰め方が見当たらないためここでおしまいです。
グラフの作り方はわかったけどここから分かることってなんだろう
最後にそのあたりも説明するね
データの見方
ヒストグラムの優れた点は、計測したデータがどこに偏って分布しているかが一目でわかるところにあります。先ほども説明しましたが、ヒストグラムはバラバラに計測された数値に区間を設定することで、各区間に該当する数値の度数をカウントします。極端な例ですが、おおむね30~80点のテスト結果を取るクラスがあったとして、0点と100点が1人ずついた場合、非常に稀有な存在であることがグラフからすぐに分かります。想定されるデータの範囲から極端に離れた数値を、統計学では外れ値と言います。今回は説明しませんが、外れ値が計測されたのが「偶然か?必然か?」といった確率を測定するための測定方法もあります。こうした確率の知識を少しかじるだけでも、宝くじやギャンブルが如何に当たらないかがすぐに分かります。
話が少し脱線しましたが、今回作成したグラフをあらためて比較してみましょう。見るべきポイントはたったの2つです。
1 山の尖り方
2 山の偏り方
山の尖り方
山の尖り方とは、「山がなだらかか?急斜面か?」ということです。両クラスの山を比較してみるとA組の山は比較的なだらかなのに対して、B組の山はとても尖っていることがお分かりになるでしょうか。
とても簡単に言うと、「A組は高得点もいる分、おバカさんもたくさんいる。B組は両極端な点数がない分、平均的な点数が高い」
ということがわかります。
山の偏り方
山の偏り方とは、山の頂点が「真ん中よりも左か?右か?」ということです。今回はヒストグラムの作成理解を優先したので偏ったグラフは避けました。この偏り方が役立つ場面としては、例えば2つのクラスでそれぞれテストの点数をヒストグラムで表現したときです。そのクラスがおおむね取るであろう点数が高ければ山は右に歪みますし、全体的に点数が低ければ山は左に歪みます。
山の尖り方・偏り方は数値で表現することが可能です。統計学の用語では尖度(せんど)・歪度(わいど)と言います。尖度と歪度は下記の記事で説明しているのであわせてお読みください。
以上の分析結果から例題の中の学年主任の先生は、
「A組は低学力の子に合わせた対策をすれば平均点の底上げができるな。B組はベースの平均点が高いので応用の教材を試してみようかな」
みたいなことが考えられるようになります。
まとめ
今回は数値データからヒストグラムを作成する方法を紹介しました。ご覧いただいてわかったかもしれませんが設定画面の入力方法さえ間違えなければとても簡単です。
ヒストグラムは統計学を学ぶうえで箱ひげ図と同じくらい最初に見方をおさえておくべきグラフです。それに今回ご紹介した内容をベースに複雑な分析方法がたくさん登場します。
私のブログでは誰でも分析ツールが使えるような説明を優先しているので難しい考え方・用語を最大限省略しています。もしきちんと座学をしたい方がいれば、統計検定3級の受験をおすすめします。よく統計学の入門として紹介されるのが統計検定2級ですが、理系出身でない方には少々ハードルお高めの内容です。そのため3級からの受験を強くお勧めしている経緯があります。
詳細は下記の記事でたっぷり説明していますのでお読みいただければ参考になると思います。
お読みいただきありがとうございました!
ありがとうございました!












ディスカッション
コメント一覧
まだ、コメントがありません