【ビジネス統計スペシャリスト対策】スプレッドシートで一元配置分散分析をする方法

はじめに
ご訪問ありがとうございます!まちゅけんです。
ヨメちゃんです。
1:スプレッドシートを使った一元配置分散分析の操作
2:一元配置分散分析の使い道
この記事ではエクセル分析スペシャリストの学習に役立つ、スプレッドシートの使い方について解説をします。今回のテーマは一元配置分析編です。Excelを使用する方法は別にご紹介をしています。
「ビジネス統計スペシャリストってなに?」という方は以下の記事を参考にして下さい。
一元配置分散分析で分かること
それでは早速、スプレッドシートを使った一元配置分散分析の操作方法について説明をします。前提として、スプレッドシートのデータ分析ツールは初期設定の状態では使うことができません。「初期設定のままだ!」という方は、データ分析ツールの有効化についてまとめた記事があるので参考にして下さい。
操作方法といっても分析をするデータがなければ何もできません。ケーススタディとして下記の事例を使ってデータ分析を行います。
とある中学3年生は1・2・3組で構成されています。ある日のこと各クラスの担任の先生は、どのクラスが一番古文の成績が優秀であるか話をすることになりました。参考にするのは最近行ったばかりの古文のテスト(100点満点)です。
1組担任「うちは点数の高い生徒が多くいるよ」
2組担任「平均的に高いのはうちかな」
3組担任「こっちは満点が2人もいるからね」
1組担任「どのクラスにも点数の高い子はいるよね。単純な平均点の比較で分かることなのかな?」
| 1組 | 2組 | 3組 |
|---|---|---|
| 80 | 85 | 100 |
| 20 | 75 | 100 |
| 10 | 70 | 65 |
| 90 | 75 | 50 |
| 85 | 70 | 75 |
| 30 | 90 | 65 |
| 80 | 65 | 70 |
| 25 | 75 | 65 |
| 30 | 80 | 60 |
| 55 | 75 | 60 |
| 10 | 65 | 55 |
| 75 | 85 | 65 |
| 70 | 85 | 55 |
| 25 | 80 | 60 |
| 90 | 70 | 65 |
| 75 | 65 | 70 |
| 85 | 75 | 55 |
| 75 | 70 | 70 |
| 80 | 65 | 65 |
| 90 | 80 | 70 |
一元配置分散分析は一言でいうと「3グループ以上あるグループ毎の平均点の差は偶然か?必然か?」を知るための分析です。今回のようなケースには打ってつけと言えます。3グループ以上と言ったのは意味があります。2グループの平均点の比較はt検定という別の検定を用いるからです。t検定は3グループ以上に対応していません。従って今回のケースでは一元配置分散分析を使うことになります。
操作方法
Anova: Single Factorを選択
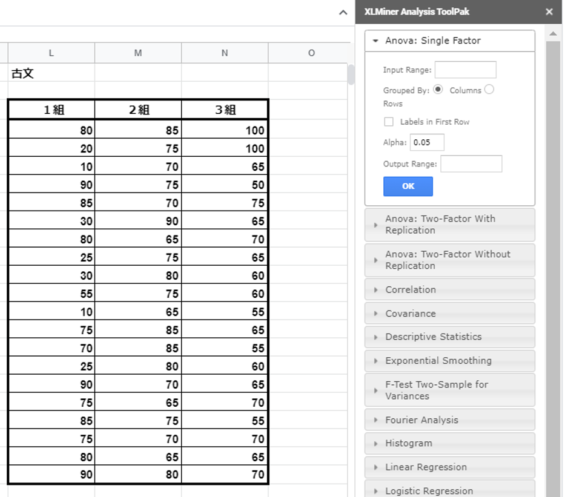
Anova: Single Factorは一元配置分散分析のことです。
範囲指定をする
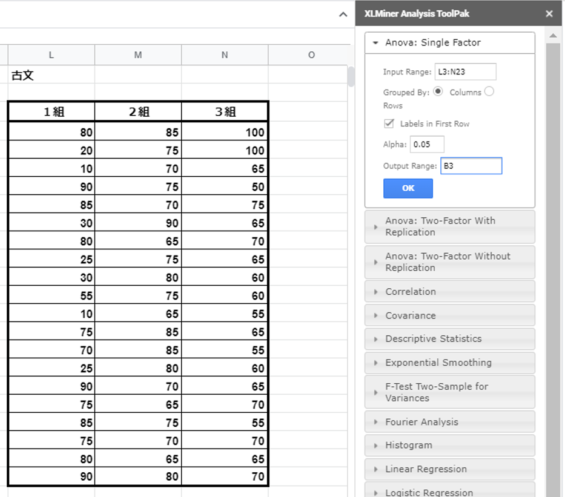
分析をするデータの範囲指定をします。3クラス分のデータを選択します。範囲指定をする際は先頭行の”1組、2組、3組”まで選択して下さい。出力するデータに名前も併せて記載するためです。範囲選択をした後にInput Rangeの横の空欄をクリックすると自動で入力されます。Output Rangeは出力先を意味しています。同じシート内で出来るだけ余白の多い場所を指定します。最後に注意点として、Labels in First Rowにチェックを入れて下さい。
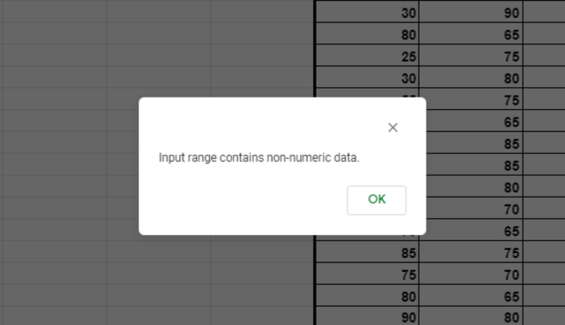
日本語では「先頭行をラベルとして使用」と言います。指定した範囲の先頭列に数字以外のデータを入れた場合は必ずチェックを入れましょう。これはスプレッドシートに対して「先頭行のデータは分析対象のグループ名だよ」と伝えることになります。チェックを入れ忘れると上の画像のようなアラートが出ます。
結果の出力
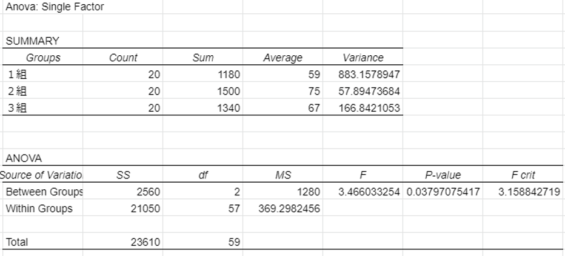
これで一元配置分散分析の操作は以上です。
データから分かること
結果は分かったけど聞いたことない単語がたくさん。
ひとによっては馴染みのない言葉ばかりかもしれないね。けど実はこの結果で見なければいけない箇所は多くないんだ。
それでは今回出力した表からわかることを解説します。表の種類は2つ。SUMMARYとANOVAです。
SUMMARY
| Groups | Count | Sum | Average | Variance |
|---|---|---|---|---|
| 1組 | 20 | 1180 | 59 | 883.16 |
| 2組 | 20 | 1500 | 75 | 57.89 |
| 3組 | 20 | 1340 | 67 | 166.84 |
これが今回の結果ですね。文字通り、1~3組ごとに古文の点数の概要です。ここで注目すべきはAverage(平均)とVariance(分散)です。この2つを組み合わせて分かることは、「各クラスの生徒の点数は平均点からどれくらいバラつきがあるか」ということです。ちなみに分散の平方根を標準偏差といいます。例えば1組の分散は883.16です。これの平方根、すなわち標準偏差は30(整数になるまで四捨五入)になります。つまり、「1組の生徒は平均点±30点の範囲にいるよ」ということが言えます。この中では2組が生徒間での点数のバラつきが小さいことが一目で確認できます。
今回の例で言うと、各生徒の点数から平均点を引き算したものを2乗して積み上げた数字のことを言います。 2乗する理由としては、生徒によっては引き算した値がマイナスになるため、2乗することでマイナスを打ち消して絶対値の合計を出すためです。なので合計した値は点数と同じ単位ではなくなります。~点として表記するためには分散の平方根、つまり標準偏差を計算します。標準偏差では~点のような単位が復活します。
ANOVA
| Source of Variation | SS | df | MS | F | P-Value | F crit |
|---|---|---|---|---|---|---|
| Between Groups | 2560 | 2 | 1280 | 3.47 | 0.038 | 3.159 |
| Within Groups | 21050 | 57 | 369.30 | |||
| Total | 23610 | 59 |
ここでも馴染みのない言葉があるかもしれませんが見てほしい数字はたったの1つ。それはP-Value(P-値)です。一元配置分散分析は 「3グループ以上あるグループ毎の平均点の差は偶然か?必然か?」 を知ることができるといいました。それをパーセンテージ化しているのがP-Valueです。「3クラスの平均点に差が出たのは3.8%の確率で偶然だよ」ということです。言い換えると「3クラスは96.2%の確率で古文の平均的に差が出る」とも言っています。つまり古文の平均点に開きが出たことには意味があると解釈するのが一般的です。今回のケースでは2組の平均点が一番高く、またクラス内のバラつきが小さいので「2組は古文において優秀」と判断をすることができます。一つ注意点を挙げると、一元配置分散分析は「3以上の複数グループのどこかに差がある」とまでしか断定ができません。従ってこれより詳細な分析をするためにはt検定という別の分析ツールを用いて、1組と2組・1組と3組・2組と3組…と総当たりで平均点の差に意味があるかを調べる必要があります。とはいえ今回のケースでは2組が優秀なのはすぐに分かりますね。
「P-Value 以外の見方を知りたい!」という方に向けてそれぞれの言葉の意味と計算方法についてまとめたので参考にして下さい。
●Source of Variation
日本語では変動要因とも言います。クラスの平均点が全体の平均点に対してどれくらいズレているかを知ることが一元配置分散分析のポイントです。
・Between Groups(各クラスの平均点と学年の平均の差)
・Within Groups(各生徒の点数と学年の平均点の差)
この二つを計算します。日本語ではグループ間・グループ内と言います。Source of VariationとはこのBetween GroupsとWithin Groupsのことを指しています。参考書によっては変動要因を因子と言ったりもします。
●SS
日本語では変動と言います。Source of Variation(変動要因)で説明したズレの計算値です。こちらも教科書によっては平方和と言うことがあります。それぞれの計算方法は下記の通りです。敢えて数式は使わずに説明をします。
・Between Groups
クラスの平均点と学年の平均点との差を2乗してクラスの人数分かけ算した値を、3クラス分合計した値です。2乗する理由としては、引き算した値がマイナスになることあるため、二乗することでマイナスを打ち消しています。
・Within Groups
各生徒の点数と学年の平均点との差を2乗した値を60人分合計した値です。2乗する理由は同じです。
●df
日本語では自由度と言います。推測統計の概念の説明が必要になるうえにそこまで重要なことではないので省略しますが計算方法は下記の通りです。
・Total (60人-1)
・Between Groups (3クラス-1)
・Within Groups (60人-1)-(3人-1)
総人数とクラス数からそれぞれマイナス1をして引き算をします。
●MS
日本語では分散と言います。SS(変動)をdf(自由度)で割った値です。
●F
日本語では分散比と言います。Between GroupsのMS(グループ間の分散)をWithin GroupsのMS(グループ内の分散)で割った値です。この数値がたまたま出る確率がP-Value(P-値)と考えて下さい。
●F crit
日本語ではF境界値と言います。F分布という説明が一から必要になるので説明を省略しますが、この値よりもFが大きければ「結果は偶然ではない」ということができます。
まとめ
スプレッドシートで一元配置分散分析をする方法について、統計学に馴染みのない方でもわかっていただけるように解説をしました。推測統計の概念や仮説検定・有意水準といったことに一切触れていませんので説明としては完全ではありません。しかしそれでいいのです。ビジネス統計スペシャリストはどんな仕事にも役立てることのできるスキルが満載です。もしも「統計学をイチから学んでみたい!」と思った方は統計検定への挑戦をオススメします。一元配置分散分析は統計検定2級相当の内容です。それ用に解説もしていますのでお読み下さい。
お読みいただきありがとうございました!
ありがとうございました!














ディスカッション
コメント一覧
まだ、コメントがありません