ビジネス統計スペシャリスト対策!スプレッドシートで共分散を求める操作方法

●スプレッドシートで共分散を求める方法
●データの読み取り方
はじめに
ご訪問ありがとうございます!まちゅけんです
ヨメちゃんです
今回はビジネス統計スペシャリストにも役立つスプレッドシートのデータ分析ツールを使って共分散を求める方法についてご紹介します。
実のところ共分散を求める問題はこの資格に登場しません。しかし敢えて紹介するからには理由があります。その理由は二つ。
1:相関関係の理解に繋がる
2:統計検定では理解必須
1:相関関係の理解に繋がる
二つのデータ群の関係性を相関といいます。そして相関の強さを数値で表したものが共分散であり、相関係数です。用語の意味は後ほど説明しますが、相関係数を求めるには共分散の算出が必要です。
確かにスプレッドシートのデータ分析ツールでは共分散をすっ飛ばして相関係数を算出できるのですが、それだと共分散と相関係数の違いも含めて「相関を理解した」とは言いづらいですよね。
2:統計検定では理解必須
もし統計検定の受験を視野に入れている場合は確実に共分散を理解しなければいけません。
スプレッドシートで簡単に計算できる相関係数ですが、共分散と二つのデータ群それぞれの分散だけを提示されて相関係数を求める問題が統計検定3級から出題されたりします。ということは、共分散とは何なのかを理解しておかなければいけません。
共分散の大切さが分かった所で、データ分析ツールを使った共分散の算出方法を解説します。
「統計検定3級ってなに?」という方は下記の記事を
「ビジネス統計スペシャリストってなに?」という方は下記の記事を参考にして下さい。
操作方法
共分散の算出方法を勉強するにあたり、今回は下記の例題を使用します。
あなたは都内にある高校1年生のクラスの担任です。最近この学校では学年テストを終えたばかり。ある日、学年主任でもある先輩とのミーティングの中で以下のような会話をしました。
学年主任「この前の学年テストどうだった?」
担任「うちのクラスでは頑張っている子と、そうじゃない子の差がハッキリと出ましたね」
学年主任「たしかにそうだったね」
担任「ひとつ言えるのが、ある科目で点数の高い子は、他のテストでも点数が高いことですね。勉強に苦手意識を持っている子もまずは1科目から頑張るように伝えられたらいいんですけど」
学年主任「そうだよね!うちのクラスでも同じ感じかなぁ。できれば生徒だけじゃなくて親御さんにもそのことを分かってもらいたいんだけど。まずは1科目から頑張れば他のテストも自然と点数が伸びるようなデータって出せたりしないかな?」
| 現代文 | 日本史 | |
|---|---|---|
| A | 80 | 150 |
| B | 70 | 160 |
| C | 40 | 90 |
| D | 60 | 140 |
| E | 90 | 190 |
| F | 70 | 170 |
| G | 60 | 140 |
| H | 80 | 170 |
| I | 50 | 110 |
| J | 70 | 140 |
共分散とは、二つのデータ群の関係性を表す数値です。「ある一方の数値が上がる時、もう片方の数値は上がる(下がる)傾向にある」という説明を数値で行うことができます。今回の例題では「現代文の点数が高い生徒は日本史の点数も高い傾向にある」ということを共分散を使って数値化したいと思います。
共分散の算出はスプレッドシート関数のCOVARIANCE.Pを使用して算出することも可能ですが、今回はスプレッドシートのアドオン(拡張機能)で使用できるXLMiner Analysis ToolPak使用します。ちなみにこのスプレッドシートのデータ分析ツールですが初期設定では使うことができません。設定方法については下記の記事を参照して下さい。
Covarianceツールを選択
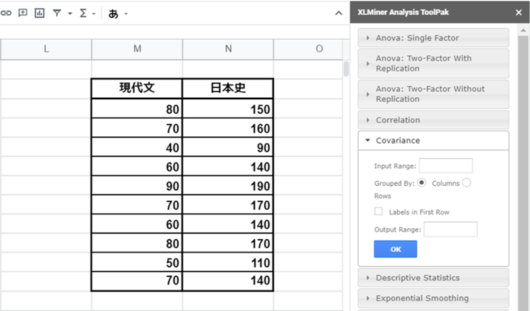
最初にスプレッドシートのデータ分析ツールを開いてCovarianceツールを選択します。Covarianceとは日本語で共分散のことです。
範囲指定をする
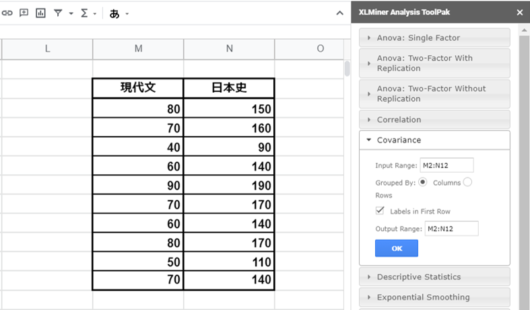
次に分析をするデータの範囲指定をします。選択列は現代文~日本史、選択行は数字の最下部までを選択します。上の画像で表示されている表はすべて選択範囲です。選択する際の注意点として、必ずLabels in First Rowにチェックを入れて下さい。
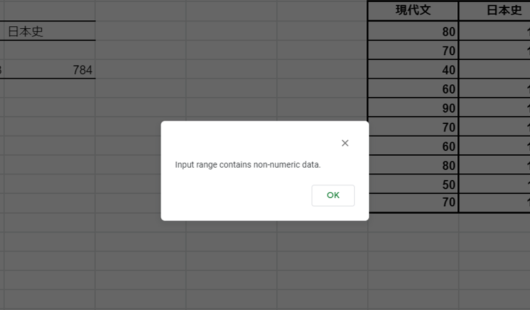
指定した範囲の先頭列に数字以外のデータを入れた場合は必ずLabels in First Rowにチェックを入れましょう。これはスプレッドシートに対して「先頭行のデータは分析対象のグループ名だよ」と伝えることになります。チェックを入れ忘れると上の画像のようなアラートが出ます。
結果が出ました!
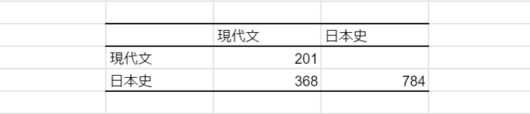
共分散を算出することができました!
簡単だよね
それぞれの数値の意味について知りたいな
データから分かること
| 現代文 | 日本史 | |
|---|---|---|
| 現代文 | 201 | |
| 日本史 | 368 | 784 |
それぞれの数値が意味するのは下記の通りです。
●201(現代文×現代文)
クラスの現代文の点数の分散
●784(数学日本史×日本史)
クラスの日本史の点数の分散
●368(現代文×日本史)
クラスの現代文と日本史の点数の共分散
分散とはクラス内でテストの点数にどれくらいバラつきがあるのかを知ることができる数値です。
例題にも登場した現代文の分散を調べるには、クラスの現代文の平均点と、各生徒の点数の差をそれぞれ二乗して合算。最後にクラスの生徒数で割った数のことをいいます。分散だけを使うことはあまりなく、分散の平方根を取った標準偏差という値を指標として用いる場合がほとんどです。
しかもクラス平均と各生徒との点数の差を二乗しているため単位が~点でありません。したがって平方根を取ることで単位を点にもどして指標を分かりやすくします。なので現代文の標準偏差は201の平方根、14点(四捨五入)となります。こうすることで「このクラスの現代文の点数は、どの生徒も平均点から前後14点以内の点数である」ということが分かります。
分散とはクラス内でテストの点数にどれくらいバラつきがあるのかを知ることができる数値です。
●分散
1:(クラスの現代文の平均点 ー 生徒の平均点)を二乗
2:1の計算をクラス全員分する
3:2で求めた値を合計してクラスの人数で割る
●標準偏差
1:分散の平方根を取る
※スプレッドシートではSQRT関数を使用すると簡単に求めることができます。
例 =SQRT(340.25)
共分散が示す意味もとても簡単です。共分散の値が0より大きいほど、現代文の点数が上がれば日本史の点数も上がる傾向(正の相関)にあります。逆に0より小さいほど、現代文の点数が上がれば日本史の点数も下がる傾向(負の相関)にあります。
先ほど求めた共分散の値は368でした。ということは正の値を取っているので、現代文と日本史の点数は正の相関にあることが分かります。つまり今回の分析結果から、「片方の点数が高い生徒は、もう片方の点数も高い傾向にある」と言うことができます。
●正の相関
片方がプラスになると、もう片方もプラスになる。
●負の相関
片方がプラスになると、もう片方はマイナスになる。
これで親御さんに、まずは1科目の勉強から頑張るように伝えることができるね
そうだね。でも実は共分散て万能じゃないんだ。そのあたりも説明するね。
共分散は万能ではない
二つのデータ群が存在するとき、データの関係性を示すために共分散は便利であることが分かりました。しかし共分散は決して万能とは言えません。それは主に2つの理由があるからです。
1:数値イメージがわかない
2:共分散同士の比較ができない
数値イメージがわかない
今回のケースだけを見れば「二つの関係性は共分散で340.25。つまり正の相関にあります!」が正解でした。しかし共分散の単位は点数ベースではありません。これだとちょっと親御さんへの説明には向かないですよね。
共分散同士の比較ができない
共分散で算出される値は比較をするデータの数値の大きさに依存します。今回のケースでは現代文(100点満点)と日本史(200点満点)の共分散を求めました。仮に現代文(100点満点)と化学(100点満点)の共分散を求めた場合、点数のベースが異なります。なので共分散同士の比較というのは基本的にしません。
また今回は学習の理解を優先したのですが、他の角度からこの分析を見た場合に「単純に現代文が得意な生徒は日本史が得意」という見方も可能です。
こうした理由から共分散は万能ではありません。ここで新たにデータの関係性の比較をする指標として相関係数が登場します。相関係数ではベースの異なる共分散を同じ指標としてパーセンテージで表現することが可能なのです。しかも様々データの関係性の強さを一覧にして示すこともできるので比較をするには打ってつけです。
共分散からの発展内容として、相関係数の求め方の解説を別にご用意しました。詳しくは下記の記事を参考にして下さい。
まとめ
スプレッドシートの分析ツール、XLMiner Analysis ToolPakを使用して共分散を求める方法を解説しました。一度ご説明はしましたが、共分散を単体で使うことはまずありません。どちらかというとその後の相関係数を求めることの方が多いかもしれません。しかしながら共分散の説明を省いて相関関係の説明をすることは出来ませんので今回のようなご説明をしました。
この記事が皆さまの統計学を理解する助けとなることを心より願っています。
ちなみに今回は Excelを使用する方法をご紹介しました。実はスプレッドシートでも全く同じことができますので、気になる方は下記の記事を参照して下さい。
もし共分散も含め、ベースから統計学の学びを深めたいという方には統計検定の受験がオススメです。以下に記事をまとめたのでご参考程度にお読み下さい、
お読みいただきありがとうございました!
ありがとうございました!















ディスカッション
コメント一覧
まだ、コメントがありません