【ビジネス統計スペシャリストに合格】Excelにデータ分析ツールを導入する方法

はじめに
この記事では下記の2点が分かります。
1:Excelでデータ分析ツールを有効にする方法
2:エクセル分析スペシャリストで使用する分析ツールの概要
ご訪問ありがとうございます!まちゅけんです。
ヨメちゃんです。
以前の記事ではビジネス統計スペシャリストについて、統計検定との違いや難易度、独学で突破するために必要なことをご紹介しました。今回からはエクセル分析スペシャリストを突破するうえでは欠かせないExcel実技の具体的な操作に焦点を絞って説明をさせていただきます。
Googleのスプレッドシートでも実は全く同じことができますので、スプレッドシートでの操作方法を知りたい方は下記の記事をお読み下さい。
そもそもとして
「ビジネス統計スペシャリストってなんだ?」
「もっと概要や勉強方法が知りたい!」
という方は下記の記事を参照して下さい。
データ分析ツールの導入方法
この試験ではExcelのデータ分析ツールを使用して様々なデータの分析をします。しかし困ったことにExcelの初期設定ではこのデータ分析ツールが有効になっていません。なのでご自身でデータ分析ツールを有効にする必要があります。しかし安心して下さい。下記の手順の通り進めていただければとても簡単です。
Excelを立ち上げる
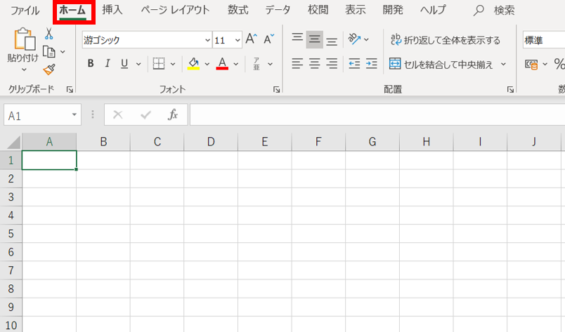
Excelを立ち上げてシートを新規作成します。すると上のような画面になりますのでホームをクリックします。
オプションを開く
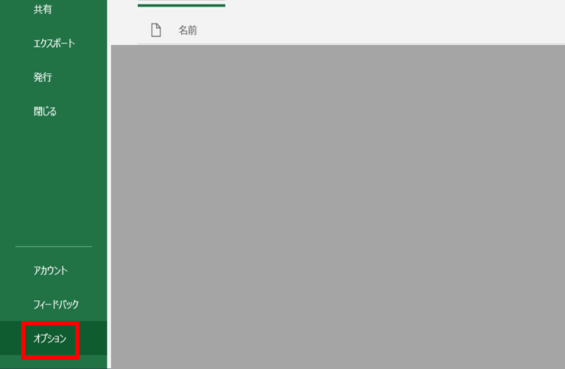
ホームをクリックしたあとの画面です。左サイドにたくさん項目が表示されるので一番下のオプションをクリックします。
アドインを選択
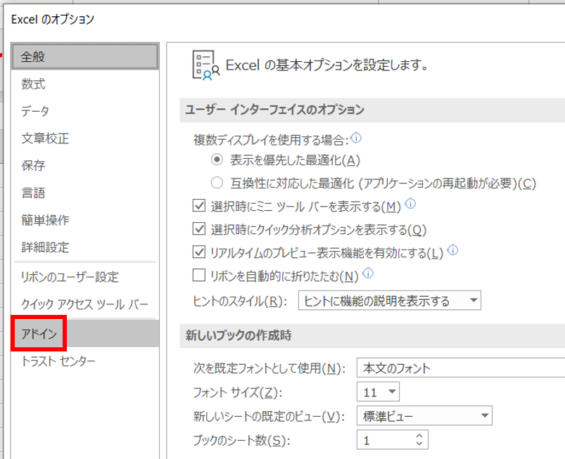
Excelのオプションを開くことができました。あと少し!
アドインという項目があるのでクリックをして下さい。
Excelアドインを有効にする
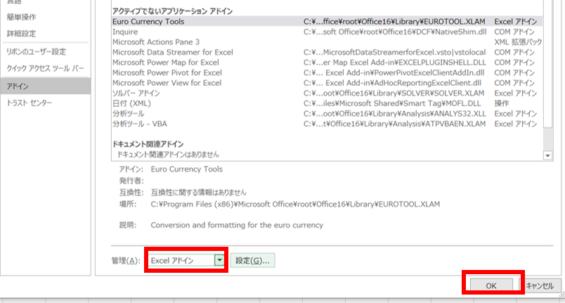
アドインをクリックすると画面が上の画像のようになります。Excelアドインを選択して、OKをクリックして下さい。
分析ツールを選択
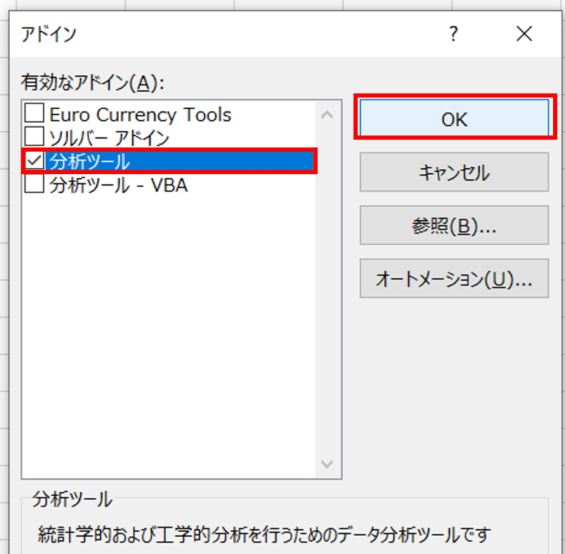
追加可能なアドイン一覧が表示されました。分析ツールを選択してOKをクリックして下さい。
※分析ツール-VBAではありません!
データを選択
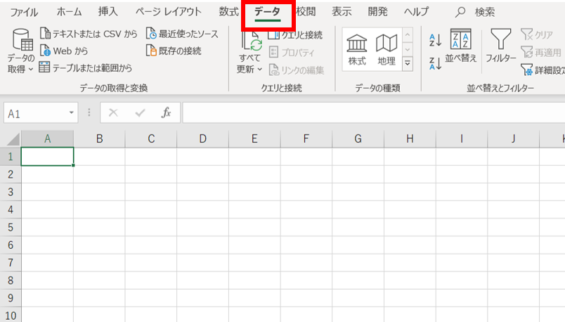
これでアドインの有効化は完了です!Excelのシート画面に戻ってデータをクリックして下さい。
データ分析を選択
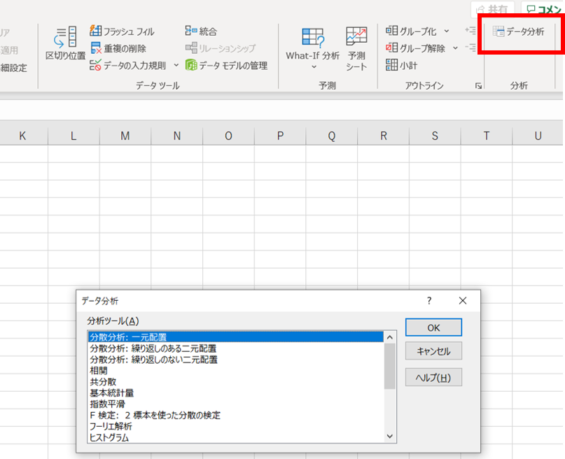
データ分析という項目が右端に追加されて様々な分析ツールが使用可能になります。これで設定は以上です!
簡単だね!
簡単でしょ。それじゃあ今度は主要な分析ツールの説明をするね。
分析ツールの説明
Excelで使用できる分析ツールは全部で19種類ありますがエクセル分析スペシャリストで使用するツールは限られています。なのでここでは実際の試験で使用するツールだけに絞ってそれぞれの用途を解説します。
●分散分析:一元配置
●相関
●共分散
●基本統計量
●F検定:2標本を使った分散の分析
●ヒストグラム
●回帰分析
●t検定
…一対の標本による平均の検定
…等分散を仮定した2標本による検定
…分散が等しくないと仮定した2標本による検定
分散分析:一元配置
3つ以上の標本の平均値を比較して有意に差があるかどうかを調べるために使用するツールです。
・・・と言うだけでは説明がパッとしませんので例え話をします。
ある小学校の6年生は1・2・3組があるとします。それぞれ担任の先生はこんな会話をします。
1組担任「国語の成績がいいのはうちのクラスだね」
2組担任「平均点はうちが一番高いよ!」
3組担任「うちのクラスには学年トップの田中と山田がいるからな」
どの先生も自分のクラスが優秀だと疑いません。そんなときに活用できるのが一元配置分散分析です。通常は各クラスの平均点を比較することを真っ先に思い浮かびますが、もしかしたら3組の担任が言っているように、特定の生徒だけがズバ抜けて優秀かもしれません。もしくは2組の平均点が一番高いと言っても1点高いだけかもしれません。このように平均点を比較するだけでは公平性に欠けていたり、たまたま出た結果かもしれない可能性を捨てきることができません。その点一元配置分散分析では、それぞれの平均点の差が生じたのはたまたまだったのかを分析することができます。
相関
片方の数値が上がるとき、もう一方の数値も上がる(もしくは下がる)傾向にあるかなど、二つの変数の関係性を調べる時に使います。
「算数の点数が高いクラスは国語の点数が高いのか」
「イケメンはバレンタインデーにチョコをたくさんもらうのか」
「気温が高い日は炭酸飲料が多く売れるのか」
など、二つの変数の関係性の強さを数値(相関係数)として表すことができます。
共分散
共分散も二つの変数の関係性を調べることに変わりはありません。
「あるクラスの国語の平均点と勉強時間の関係性を調べたい」といった時は共分散を使用します。
共分散が正の値を取る時、勉強時間が増えるほど国語の点数は増えます。逆に共分散が負の値を取る時は、勉強をするほど国語の点数が下がることになってしまいます。
「え、じゃあ相関係数っていらなくない?」と思うかもしれませんが実はそうでもありません。
共分散では国語の平均点と勉強時間の関係性を表すことができると言いました。では算数&勉強時間と国語&勉強時間ではどちらの関係性が強いのかを考えます。残念ながら共分散を比較するだけでは関係性の強さを比較することができません。共分散は国語&勉強時間のようにワンペアでの関係性の強さを知ることしかできないため、全く指標のことなる国語と算数を比較できないのです。ここで活用できるのが相関係数です。相関係数では国語と算数の指標の違いも加味した計算式を使うため、関係性の違いを比較することができます。
基本統計量
データの基本的な特性を算出することができます。例えるならデータのプロフィールです。
47都道府県ごとに全てのコンビニの1日の売上を比較するとします。
「一番売り上げの高い店舗は何県にある?」
「売上の開きが一番大きいのは何県?」
「店舗数が一番少ないのは何県?」
「県内で一番売り上げのバラつきがあるのは何県?」
みたいな疑問は全て基本統計量が解決してくれます。
・平均
・標準誤差
・中央値
・最頻値
・標準偏差
・分散
・尖度
・歪度
・範囲
・最小
・最大
・合計
・データの個数
F検定:2標本を使った分散の分析
二つの標本の分散が等しいかを調べる分析です。大体はt検定の前に使用します。
「営業部と企画部の給料ではどちらにバラつきがあるだろうか」みたいなことを考えたいときにはF検定が便利です。仮に営業部と企画部では平均給料が同じでも、営業部では極端に多いひとや少ないひとがいるかもしれません。F検定ではそういった部毎に給料のバラつきが等しいかを知ることができます。
ヒストグラム
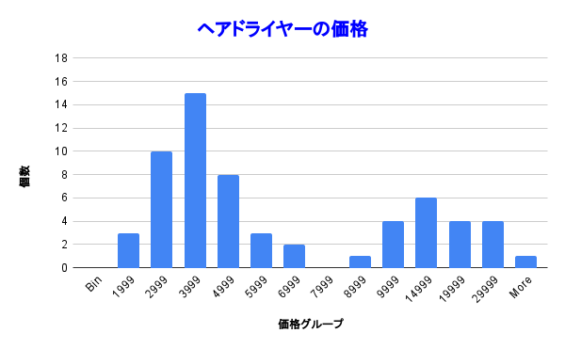
こんな感じのグラフを見たことがありますでしょうか。これがヒストグラムです。あるデータの集まりを区間ごとに区切ってカウントしたものを見える化したものを指します。
回帰分析
結果の数値と、その数値を生み出した原因の関係を導き出すためのツールです。
「晴れと雨ではお店の売上がいくら変わるか?」
「メールとハガキではどちらが集客になるか?」
「駐車場が一番混むのは何曜日か?」
といった関係性を数式化して求めることができるのが回帰分析です。
t検定
二つの標本データの平均を比較するのがt検定です。
「ニつの平均値が異なっていることに意味があるか?偶然か?」
みたなことを知ることが出来ます。また用意する標本によって使用するツールは異なります。具体例も交えると以下の通りです。
●一対の標本による平均の検定
一対の標本というのは比較をするデータの発生源が同じものを指します。対応のあるデータと言ったりもします。あるクラスの授業前と後のテストの成績を比較したり、ダイエット食品の使用前と使用後の体重変化などが該当します。
●等分散を仮定した2標本による検定
一対の標本ではない場合の平均の検定を指します。男女の身長差、日本とアメリカの所得差、工場Aと工場Bの生産量の差などがあたります。ポイントは、ニつの標本の分散が等しいと仮定をして計算をすることです。t検定の前にF検定を通じて等分散の有無を調べます。このt検定は別名スチューデントのt検定と呼ばれています。
●分散が等しくないと仮定した2標本による検定
このt検定ではニつの標本の分散が等しくないと仮定をして検定を行います。一般的には等分散を仮定しないツールを使うことの方が多いようです。ウェルチのt検定とも言います。
まとめ
さて、Excelでデータ分析ツールを有効にする方法と、ビジネス統計スペシャリストで使用する分析ツールについて簡単な解説をしました。次回からは各分析ツールの操作方法について、今回同様に画像を通じてご説明をします。実際の試験でつまづきやすいポイントも紹介しますので楽しみにしていて下さい。
ビジネス統計スペシャリストに興味が沸いた方は以前書いた記事を参考にして下さい。
統計学はデータサイエンティストなど一部の職業に限った知識ではなく、私たちの普段の仕事にも大いに役立つ学問です。この記事をきっかけに興味を持っていただければ嬉しい限りです。
お読みいただきありがとうございました!
ありがとうございました!












ディスカッション
コメント一覧
まだ、コメントがありません